Calculs des paramètres S d’un quadripôle et mesure par le LiteVNA.
- xaviermotti
- 29 oct. 2025
- 6 min de lecture
Le fichier est téléchargeable à la fin du post.
Ce post est dédié à l'utilisation du LiteVNA. Dans ce post, je cherche à comprendre la mesure des coefficients S11 et S21 proposés par le VNA et de les comparer au résultats des calculs.
J'utilise trois sortes de quadripôles : - purement résistif - inductif - capacitif

-1- Présentation du VNA
-1- Présentation du VNA
1.1- Généralités.
Le VNA ou Vector Network Analyser = analyseur vectoriel de réseau est un appareil de mesure qui scanne un circuit électrique sur une plage de fréquence prédéfinie :
- sur son port S1, il fournit au circuit une tension sinusoïdale de fréquence, d'amplitude et de phase connues ;
- sur son port S1, il mesure l'amplitude et la phase des tensions et courants incidents et réfléchis ;
- sur son port S2, il mesure l'amplitude et la phase de la tension et du courant du signal transmis.
1.2- Les paramètres affichés sur l'écran.
Le VNA propose l'affichage de nombreux paramètres, je me focalise sur les deux paramètres S :
- S11 qui est défini comme un coefficient de réflexion
- S21 qui est homogène à un gain en puissance
Pour ma propre compréhension des informations affichées sous S11 et S21, je me propose de comparer les valeurs fournies par le VNA à mes calculs.
Les calculs sont détaillés dans le document PDF en téléchargement à la fin de ce post.
-2- Relations utilisées dans les calculs.
Biblio 1 page 26-28.
Nous aurons besoin des trois relations suivantes :

Dans lesquelles a1, b1 sont les ondes incidentes et réfléchies en entrée
a2, b2 sont les ondes incidentes et réfléchies en sortie
Ze est l'impédance, vue de l'entrée, du quadripôle débitant sur la charge R2
Zs est l'impédance, vue de la sortie, du quadripôle débitant, en entrée, sur la charge R1 (E=0)
Remarque : dans tout le post, les lettres majuscules (ex. V2, Z ...) sont des valeurs complexes.
-3- Etude du paramètre S11
3.1- Coefficient de réflexion S11 : circuit purement résistif.
Le schéma 1 du montage testé est le suivant :

Réglages.
On peut définir une nouvelle impédance interne du port S1 et du port S2 avec la commande : PORT-Z.
Dans tous les cas, PORT-Z s'applique à la fois à S1 et à S2.
Données : PORT-Z = 50 ohm ; fréquence : f = 5,0 MHz ;
On utilise la relation (1) de la biblio.1.
Mesure de S11 avec le Lite VNA S11 = 0,242 + j0,000456 = 0,242 + j0
Calculs.
Ici la résistance équivalente à Rc//R2 vaut 100 // 50 = 33,3 ohm

Les écarts entre ces deux chiffres s'expliquent probablement par le comportement réel des résistances à la fréquence f = 5,0 MHz.
3.2- Coefficient de réflexion S11 : circuit inductif.
Le schéma 1 du montage testé est le suivant :

(E, R1) est en pointillés car c'est le générateur intégré à S1 au VNA ;
R2 est aussi en pointillés car c'est l'impédance du récepteur intégré à S2.
Données : f = 5,0 MHz ; XL = jLw = j36,4 ohm ; Port-Z = 50 ohm ;
Par le calcul on trouve :

A la mesure au VNA : S11 = 99.2m + j301m = 0,0992 + j0,301
3.3- Coefficient de réfléxion S11 : circuit capacitif CR.
Le schéma du montage testé est le suivant :

(E, R1) est en pointillés car c'est le générateur intégré à S1 au VNA ;
R2 est aussi en pointillés car c'est l'impédance du récepteur intégré à S2.
Données : f = 5,0 MHz ; XL = 1/jCw = -j67,7 ohm ; R'2 = 33,3 ohm
Ici R'2 est la résistance équivalente à l'association parallèle R = 100 ohm et R2 = 50 ohm
Par le calcul on trouve :

A la mesure au VNA : S11 = 0,287 - j.0,587
Je trouve une bonne coïncidence entre mesure et calculs.
3.4- Conclusion.
Les mesures de S11 fournies par le LiteVNA sont cohérentes avec la définition (théorique) du paramètre de dispersion S11.
-4- Etude du paramètre S22
Le coefficient S22 est le coefficient de réflexion vu depuis la sortie.
Pour l'obtenir, il suffit donc de retourner le quadripôle, c'est à dire de l'alimenter par la sortie.
Voyons cela sur l'un des montages précédents.
On utilise la relation (2) de la biblio.1.
4.1- Coefficient de réflexion S22 : circuit inductif.
S22 est le paramètre S pour le quadripôle vu depuis la sortie. Pratiquement, cela revient à permuter entrée et sortie.
Le schéma 1 du montage testé est le suivant :

Pour ce quadripôle parfaitement symétrique de celui du 3.2-, les mesures vues de la sortie seront identiques à celles vues de l'entrée, dans ce cas : S22 = S11.
4.2- Coefficient de réflexion S22 : circuit capacitif.
Vue de la sortie, le circuit du 3.3- est le suivant :

Données : f = 5,0 MHz ; Port-Z = 50 ohm ; Réactance Xc = -j67,7 ohm
Pour ce quadripôle on calcule d'abord l'impédance Zs vue depuis la sortie :

Pour la mesure au VNA, je trouve : S22 = 12,4m - j249m = 0,0124 - j0,249
Ici aussi, la coïncidence avec le calcul est correcte si l'on admet que la valeur de la capacité C du condensateur est connue avec peu de précision.
-5- Etude et mesure de S21
5.1- Coefficient de transmission S21 : circuit purement résistif.
Le schéma 1 du montage testé est le suivant :

Données : Port-Z = 50 ohm donc R1 = R2 = 50 ohm ; f = 5 MHz ;
Calculs : On utilise la relation (3) de la biblio.1.

Le circuit étant purement résistif S21 est une valeur réelle.
Mesure avec le Lite VNA S21 Polar S21 = 8248m - j18m = 0,825 - j0,018
S21 Linear S21 = 0,825 semble être le module de S21 Polar
Le LiteVNA traduit aussi l'information sous la forme :
S21 Smith shunt S21 = 116 - j14,5 ohm
et S21 Serie R = 21,2 ohm et X = 2,64 ohm
qui représentent probablement une impédance équivalente série ou parallèle du quadripôle.
Je suppose que le but est de permettre d'autres calculs. Je n'ai pas encore approfondi cette information.
5.2- Coefficient de transmission S21 : circuit inductif.
Le schéma 1 du montage testé est le même que celui du 3.2-

Données : PORT-Z = 50 ohm ; fréquence f = 10,0 MHz ; Réactance bobine XL = j72,9 ohm
Calculs : On utilise la relation (3) de la biblio.1.

Mesure de S21 avec le Lite VNA S21 = 0,698 - j0,457 polar à f = 10 MHz

L'égalité est encore une fois correctement vérifiée : l'erreur la plus grande est commise sur l'inductance L.
A 10 MHz on peut également s'attendre que les résistances aient une composante réactive.
Le VNA propose une mesure de S21 Smith R+JX shunt qui donne :
S21 = 0,243 + j65,7 W R et X serie
Cette valeur correspond à la réactance XL d'une bobine de 1,05 µH.
La valeur de la résistance R me parait correcte car le circuit est court.

5.3- Coefficient de transmission S21 : circuit capacitif
Le schéma 1 du montage testé est celui du 3.3-

Données :
PORT-Z = 50 ohm ce qui entraîne R1 = R2 = 50 ohm
Fréquence f= 10,0 MHz
Réactance du condensateur Xc = -j67,7 ohm
Calculs.
Relations et démarche : Biblio.2. p10-12
Dans un premier temps, il faut déterminer la relation entre V2 et E.
On transforme le réseau série C-Rb en réseau parallèle C'R'b pour la fréquence de travail fsoit : C' = 484 pF ; R'b = 111,5 ohm à f = 10 ,0 MHz
Le circuit se transforme en :

On nomme Z l'association parallèle : Ra//R'b//R2//Xc'
Z = 16,9 + j12,9 ohm
Z est ensuite utilisé dans le pont diviseur de tension pour le calcul de V2 :
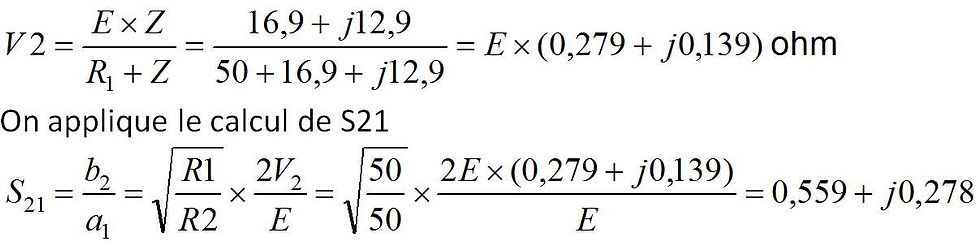
Mesure de S11 avec le Lite VNA S21 = 0,5832 linear
S21 = 0,526 + j0,251 polar

Les résultats des mesures sont assez proches des calculs. La précision des calculs est toujours confrontée aux erreurs sur la valeur des composants notamment dûe aux effets de la fréquence et sur la propagation des erreurs par les formules.
-6- Conclusion générale
Pour les exemples présentés, le LiteVNA permet d'obtenir les paramètres S11 et S21 d'un quadripôle, conformément aux relations théoriques.
On peut également déterminer expérimentalement S22 en retournant le quadripôle.
Le plus grand accord entre calculs et mesure est obtenu avec les réseaux purement résistifs. Cela ne nous surprend pas car l'erreur sur la valeur des composants est la plus faible.
Pour le cas de la bobine, nous partons d'une valeur L = 1,16 µH (inductancemètre) qui est estimée à 1,05 µH par le VNA soit une erreur initiale de 11%.
Cette erreur est très certainement encore plus élevée pour la capacité C du condensateur..
Toutes les expériences ont été faites sur des quadripôles passifs. Utiliser le LiteVNA sur des quadripôles actifs doit être fait avec réflexion car il y a un risque de saturation et surtout de destruction de l'étage d'entrée si des signaux trop élevés lui sont appliqués.
Le calcul des paramètres S11 et S21 pour un circuit complexe devient très lourd. Je ne l'ai pas envisagé pour l'instant ...
Bibliographie
1- Electronique Radiofréquence. André PACAUD. Série Technosup chez Ellipse. juillet 2011. ISBN 978-2-7298-0073-4
2- Radiofréquence et télécommunications analogiques. Gérard PRIEUR. Masson 1996. ISBN 2-225-85380-0 ISSN 1272-2073



Commentaires